Anomaly detection is an important topic in computer science. This article presents a few most common approaches to this problem, and shows an example of a simple autoencoder used for this purpose.

Anomaly detection means finding those elements in a dataset, which in some way are not typical for the given set. This problem has a wide variety of use cases :

• intrusion detection
• system health monitoring
• detection of medical issues
• fraud detection
• telecommunication network malfunction detection
• products quality defects detection

Most popular for this purpose are unsupervised methods of machine learning – this approach has several advantages over supervised learning, as it does not require a labeled dataset to learn what is a regular element and what is an anomaly – it bases on the assumption, that most elements in the dataset are not anomalous, and based on this the algorithm tries to learn what is normal. Also, it does not need examples of anomalies for training, unlike supervised algorithms.

Common methods

There are countless anomaly detection methods. Among the most popular ones are:

• Density-based methods
• k-nearest neighbor – a simple method that relies on calculating the distance between points in multidimensional space. It assumes that data can be grouped in a way in which distances between elements in a group are relatively small, and elements which are not included in any group could potentially be anomalies.
• __Local Outlier Factor __ – for each element the distance to some predefined number of closest elements is calculated in order to calculate the density of data around this element. If the density is low, the element can be an outlier.
• Isolation forests – a collection of decision trees is created, and each decision tree splits the data into two parts along a randomly selected value of a randomly selected dimension. When data is divided, most isolated points are potential anomalies.
• Density Based Spatial Clustering of Applications with Noise (DBSCAN) – the algorithm is parametrized by two variables: maximum distance between points to consider them neighbors, and minimal number of points to form a cluster. Based on their values, clusters are formed. When new data comes, and it does not fall within any cluster, it is an outlier.
• One-Class Support Vector Machine – this unsupervised modification of regular SVM bases on finding a hyperplane that contains all the elements from the training data, so when new data comes, and lies outside of the hyperplane, it’s considered outlier.
• Autoencoder – a neural network consisting of an encoder and a decoder. Its goal is to reduce dimensionality of input data and reconstruct it with as little loss as possible. The autoencoder is trained in an unsupervised manner – it extracts features that are common for training data, and that allows it to reconstruct data similar to those from training set pretty well, but when input that is to be reconstructed is significantly different from training data, the autoencoder is unable to compress and reconstruct it properly – that’s why by measuring reconstruction loss it’s possible to determine if input data is an anomaly.

Let’s implement an autoencoder!

Now it’s practice time! Let’s implement a really simple anomaly detection algorithm using an autoencoder in TensorFlow. We will use the MNIST dataset, which is probably known by thise, who have ever done anything related to machine learning. For those, who haven’t – it’s a collection of 10,000 images of handwritten digits, which is most commonly used for image recognition. For the sake of simplicity, we will train the model only for images of zeros from the dataset, so every other number would be considered an anomaly.

First things first – we need to import necessary components.

import matplotlib.pyplot as plt
import tensorflow as tf

from tensorflow.keras import layers, losses
from tensorflow.keras.models import Model
from tensorflow.keras.datasets import mnist

Now we will prepare data…

(data_train, labels_train), (data_test, labels_test) = mnist.load_data()

mnist_zeros_train = data_train[labels_train == 0]
mnist_zeros_test = data_test[labels_test == 0]
mnist_ones_test = data_test[(labels_test == 1)]

mnist_zeros_train = mnist_zeros_train.astype('float32') / 255.
mnist_zeros_test = mnist_zeros_test.astype('float32') / 255.
mnist_ones_test = mnist_ones_test.astype('float32') / 255.

mnist_zeros_test_size = len(mnist_zeros_test)
mnist_ones_test_size = len(mnist_ones_test)

…and create and train our simple autoencoder, which has one fully connected layer with ReLU activation in the encoder, and one fully connected layer with sigmoid activation in the decoder. In this example the encoder will compress the input to 16 dimensions, but feel free to play with other values. You can also play with the structure of the autoencoder itself, and examine how it changes the outcome.

encoded_dim = 16


class Autoencoder(Model):
    def __init__(self, encoded_dim):
        super(Autoencoder, self).__init__()
        self.latent_dim = encoded_dim
        self.encoder = tf.keras.Sequential([
            layers.Flatten(),
            layers.Dense(encoded_dim, activation='relu'),
        ])
        self.decoder = tf.keras.Sequential([
            layers.Dense(784, activation='sigmoid'),
            layers.Reshape((28, 28))
        ])

    def call(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return decoded


autoencoder = Autoencoder(encoded_dim)

autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())

We use the same data as input and as output, because we want our autoencoder to reconstruct its input to an output with as high precision as it can.

autoencoder.fit(mnist_zeros_train, mnist_zeros_train,
                epochs=10,
                shuffle=True,
                validation_data=(mnist_zeros_test, mnist_zeros_test))

Now, when our model has been trained, let’s test how well it can reconstruct images of zeros.

reconstructions_zeros = autoencoder.predict(mnist_zeros_test)
reconstructions_zeros = tf.reshape(reconstructions_zeros, [mnist_zeros_test_size, 28 * 28])
mnist_zeros_test = tf.reshape(mnist_zeros_test, [mnist_zeros_test_size, 28 * 28])
zeros_loss = tf.keras.losses.mse(reconstructions_zeros, mnist_zeros_test)

plt.hist(zeros_loss.numpy(), bins=30, range=[0, 0.15], color='blue')
plt.xlabel("Reconstruction loss of valid data")
plt.show()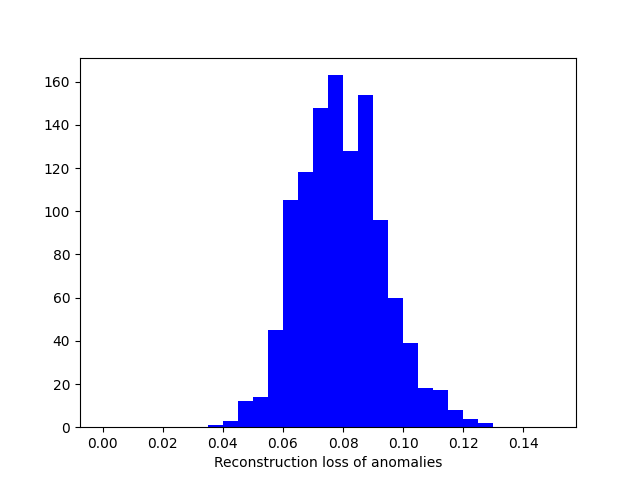

We can see that reconstruction loss is significantly larger for anomalies, and now all we have to do is to set some threshold above which we consider an example an anomaly – based on the histograms, it would be around 0.04.

Conclusion

Anomaly detection is a really significant branch of data science, and is approached in large number of ways. The autoencoder is one of them, and a very popular one, and as it can be seen here, it’s really easy to implement a basic autoencoder with TensorFlow. But don’t forget that beyond autoencoders and other methods mentioned before, anomaly detection is such a wide topic that it would take a whole book to cover it, while this post is just scratching the surface.